Gauss–Hermite quadrature
In numerical analysis, Gauss–Hermite quadrature is an extension of Gaussian quadrature method for approximating the value of integrals of the following kind:
In this case
where n is the number of sample points to use for the approximation. The xi are the roots of the ("physicists'") Hermite polynomial Hn(x) (i = 1,2,...,n) and the associated weights wi are given by [1]
References
- ^ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN 978-0-486-61272-0. Equation 25.4.46.
Further reading
- § 3.5. Quadrature: Gauss–Hermite Formula at the Digital Library of Mathematical Functions
- For tables of Gauss-Hermite abscissae and weights up to order n = 32 see http://www.efunda.com/math/num_integration/findgausshermite.cfm.
External links
- Generalized Gauss–Hermite quadrature, free software in C++, Fortran, and Matlab
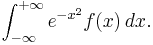
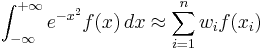
![w_i = \frac {2^{n-1} n! \sqrt{\pi}} {n^2[H_{n-1}(x_i)]^2}.](/2012-wikipedia_en_all_nopic_01_2012/I/9b88c3ab14d2a3574ebaafb9fef1c033.png)